Цепи переменного тока.
Резистор.
Мы уже знаем как ведет себя резистор в цепи постоянного тока, рассмотрим как он поведет себя в цепи переменного тока: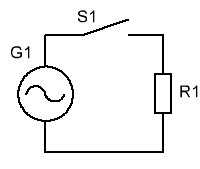
Построим график напряжений и токов простейшей резистивной цепи:
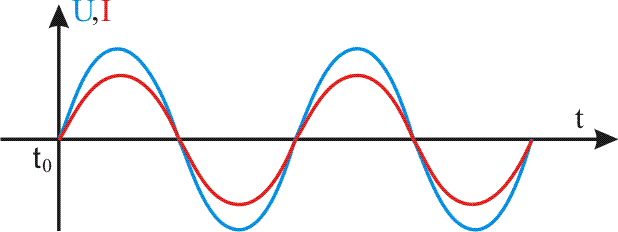
Поскольку резистор оказывает непосредственное сопротивление потоку электронов,
волна напряжения на этом резисторе совпадает по фазе с волной проходящего через
него тока. Мы можем взять любой момент времени на горизонтальной оси графика и
сравнить значения тока и напряжения в этот момент друг с другом (такие значения
называются мгновенными, так как определяются они для произвольного момента
времени). Когда мгновенное значение тока равно нулю, мгновенное значение
напряжения так же равно нулю. Аналогично, в момент времени, когда ток через
резистор имеет максимальное положительное значение, напряжение на нем также
имеет максимальное положительное значение. Отсюда можно сделать вывод, что
закон Ома сохраняет свою справедливость для мгновенных значений напряжения и
тока в любой момент времени.
Можно рассчитать рассеиваемую мощность P резистора и нанести её на график:
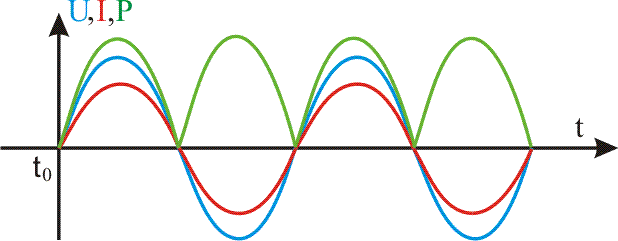
Обратите внимание на то, что мощность никогда не принимает отрицательных
значений. Если ток положителен, то напряжение также положительно, а это значит,
что мощность тоже принимает положительное значение (P = IU). И наоборот, если
ток отрицателен, то напряжение также отрицательно, а умножение двух
отрицательных чисел дает нам в итоге положительное число. Из всего
вышесказанного можно сделать вывод, что резистор ведет себя одинаково и
в цепях постоянного тока и в цепях переменного тока, он всегда рассеивает
мощность, принимая её от источника и превращая её в тепловую энергию.
Но не все компоненты ведут себя одинаково в цепях постоянного и переменного тока,
например трансформатор, прекрасно работающий с переменным током - не работает в
цепи с постоянным током. А резистор, его еще называют активным сопротивлением,
или лампа накаливания прекрасно работают и на постоянном и на переменном токе.
Конденсатор.
Сначала рассмотрим как поведет себя конденсатор в цепи постоянного тока: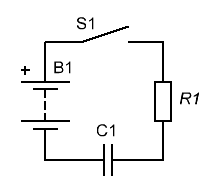
Очевидно, что когда выключатель S1 замкнут, тока в цепи также не будет,
так как ток просто не сможет пройти через диэлектрик, который разделяет
пластины конденсатора. Но давайте внимательно рассмотрим что происходит
в момент её включения. Для этого построим график, по оси Х которого будем
откладывать время, а по оси Y - отложим напряжение (синий график) и ток
(красный график), измерять будем прямо на конденсаторе.
Момент включения - в начале координат, t=0.
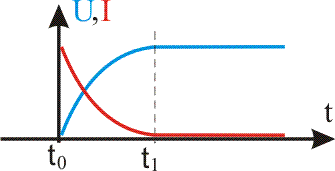
Итак, в исходном состоянии, конденсатор разряжен, напряжение на нем равно нулю,
тока в цепи тоже нет, так как выключатель разомкнут. В момент включения (t=0),
конденсатор начнет заряжаться и через какое-то время, обозначим его t1,
конденсатор зарядится полностью и напряжение на его обкладках будет такое же как
на полюсах источника питания (синий график). Ток же напротив, в начале он будет
принимать максимальное значение, но по мере заряда конденсатора он будет
уменьшатся, и станет равным нулю когда конденсатор зарядиться (красный график).
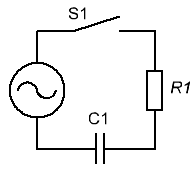
Теперь рассмотрим конденсатор в цепи переменного тока, заменим батарейку
генератором переменного тока:
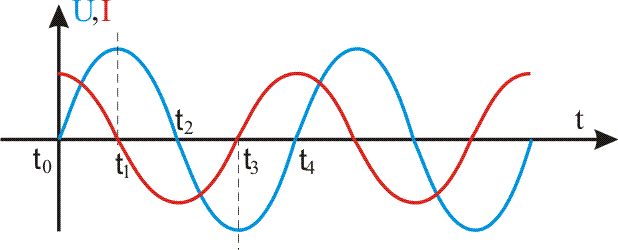
Возьмем за начальный момент времени t0 момент, когда мгновенное
значение переменного тока переходит через ноль из отрицательного значения к
положительному. В этот момент конденсатор начнет заряжаться, и фактически будет
следовать за напряжением генератором (синий график). Естественно ток, по мере
заряда конденсатора будем уменьшатся и когда конденсатор зарядится, на какой-то
момент ток станет равным нулю (красный график). Это так называемый зарядный ток.
А вот дальше начинается самое интересное, напряжение генератора достигнув в
момент времени t1 максимального положительного значения, начинает
уменьшатся. При этом, конденсатор, будучи также максимально заряженным - начнет
разряжаться, в цепи начнет появляться ток разряда, но направлен он будет в
обратную сторону, о чем говорит красный график, который пройдя через ноль,
попадает в отрицательную область. Ток достигнет своего максимального значения,
когда конденсатор полностью разрядится, в момент времени t2.
Разрядившись, конденсатор начнет снова заряжаться, но уже отрицательным
напряжением, так как мгновенное значение напряжения генератора пройдя через
ноль примет отрицательное значение. В момент времени t3, конденсатор
полностью зарядится, ток опять на мгновение примет нулевое значение. Далее
процесс пойдет в обратном направлении, мгновенное напряжение генератора,
достигнув своего максимального отрицательного значения, опять начнет уменьшатся,
а конденсатор опять начнет разряжаться, при этом ток начнет увеличиваться,
при этом в момент времени t4 конденсатор окажется полностью
разряженным, ток достигнет своего максимального значение и процесс опять начнет
повторяться. Таким образом, полный цикл, который составляет 360°, и который
состоит из четырех равных по времени участков, каждый по 90° :
t0-t1, t1-t2,
t2-t3, t3-t4.
Подведем итог, он очень важен и прост. Если на конденсатор подано переменное
синусоидальное напряжение, то через него будет идти синусоидальный ток, при
этом значение этого тока будет зависеть от ёмкости конденсатора. Но самое
главное, ток опережает напряжение на четверть периода, или на 90 градусов.
Это не нужно понимать так, как будто ток появляется раньше, чем мы прикладываем
к конденсатору напряжение, это невозможно. Просто амплитуда тока наступает на
четверть периода раньше, чем амплитуда напряжения.
Тот факт, что конденсатор влияет на величину переменного тока в цепи, уже
чем-то напоминает известный нам закон Ома, где ток зависит от сопротивления
цепи. В цепи переменного тока, конденсатор можно рассматривать как особое,
ёмкостное сопротивление, которое обозначается XC. При этом,
ёмкостное сопротивление XC зависит от ёмкости конденсатора C и от
частоты f переменного тока. Это очень просто объяснить, с увеличением ёмкости
конденсатора, при одном и том же напряжении, он может принять на свои обкладки
больше зарядов, поэтому зарядный и разрядный ток будут больше. А раз ток
растет, значит, согласно закону Ома сопротивление, в данном случае ёмкостное
сопротивление XC, стало меньше.
Величина тока также зависит и от того, с какой скоростью меняется напряжение.
Чем больше скорость, тем больше зарядов за одно и тоже время приходит на
обкладки конденсатора и уходят с них, следовательно, больше ток. А чем больше
ток - тем меньше сопротивление. Следовательно, ёмкостное сопротивление
XC зависит от частоты f - чем больше частота f, тем быстрее меняется
переменное напряжение, тем больше ток в цепи конденсатора, а значит, меньше
ёмкостное сопротивление XC
где XС - сопротивление (Ом), f - частота (Гц), C - ёмкость (Ф).
Катушка.
Теперь рассмотрим как поведет себя катушка в цепи постоянного тока: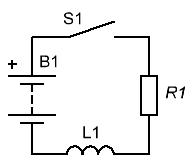
Очевидно, что когда выключатель S1 замкнут, тока в цепи будет максимальный,
а напряжения на катушке будет минимально, почти равное нулю, так как
сопротивление провода из которого сделана катушка очень мало.
Но если рассмотреть что происходит в момент включения, то выяснится
довольно любопытная вещь. Построим график, по оси Х которого будем
откладывать время, а по оси Y - отложим напряжение на катушке (синий график)
и ток в цепи (красный график). Момент включения - в начале координат, t=0.
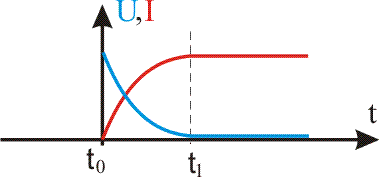
В исходном состоянии, тока в цепи нет, так как выключатель разомкнут. В момент
включения (t=0), в катушке начинает протекать ток, который создает вокруг неё
магнитное поле и одновременно образуется ЭДС самоиндукции, которая будет
препятствовать мгновенному нарастанию тока в катушке. Нарастание тока
происходит постепенно, но через некоторое время, обозначим его t1,
переходной процесс закончится, и ток достигает своего максимального значения
(красный график), а напряжение на катушке будет уменьшаться (синий график).
Теперь рассмотрим поведение катушки индуктивности в цепи переменного тока,
заменим батарейку генератором переменного тока:
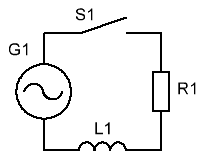
Возьмем за начальный момент времени t0 момент, когда мгновенное
значение переменного тока переходит через ноль из отрицательного значения к
положительному. В этот момент напряжение на катушке будет максимально, а
через катушку начинает течь ток, создавая вокруг нее магнитное поле и порождая
ЭДС самоиндукции, препятствующий нарастанию тока в катушке.
Ток, в первой четверти периода (t0 - t1),
противодействующей ЭДС самоиндукции, максимальный и противоположный по знаку
с напряжением на катушке. В следующую четверть периода
(t1 - t2), когда напряжение на катушке
индуктивности уменьшается, магнитное поле индуцирует ЭДС самоиндукции,
которое совпадает с направлением тока. Этот ток самоиндукции
в катушке старается уже "помочь" уменьшающему переменному току сохранить
достигнутый большой магнитный поток. В этот полупериод катушка индуктивности
уже не потребляет, а отдает энергию обратно генератору. Далее процесс
будет повторяться уже с обратным знаком.
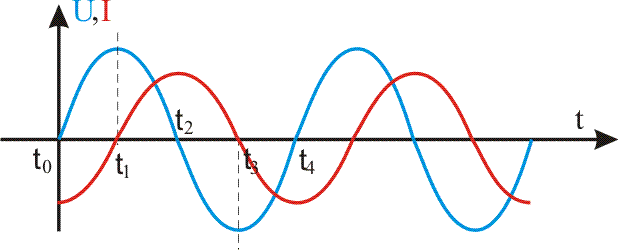
Подведем итог. Если на катушку подано переменное синусоидальное напряжение,
то через неё будет идти синусоидальный ток, при этом значение этого тока будет
зависеть от индуктивности катушки. Но самое главное, ток будет отставать от
напряжения на четверть периода, или на 90 градусов.
В цепи переменного тока, катушку, как и конденсатор можно рассматривать как
особое, индуктивное сопротивление, которое обозначается XL. При этом,
индуктивное сопротивление XL зависит от индуктивности L и от
частоты f переменного тока. Это очень просто объяснить, с увеличением
индуктивности катушки, при одном и том же напряжении, ток будет нарастать более
медленно, а значит, согласно закону Ома сопротивление, в данном случае
индуктивное XL, будет больше.
где XL - сопротивление (Ом), f - частота (Гц), L - индуктивность (Г).
Индуктивное сопротивление XL похоже на емкостное сопротивление
XC тем, что зависит от частоты. Но если с увеличением частоты f
сопротивление XC падает, то XL - растет. Катушка, если
пренебречь сопротивлением провода, из которого она изготовлена, так же как и
конденсатор, оказывается не активным, а реактивным элементом цепи.
При этом, реактивное сопротивление хот и влияет на величину тока, но мощности
от генератора не потребляет. Все что катушка отбирает от генератора на
создание магнитного поля - она затем возвращает обратно, так же как и
конденсатор отдает в цепь накопленный в электрическом поле заряд.
Copyright © R9AL 2020 Все права защищены
