Последовательный колебательный контур.
Мы уже выяснили, что реактивные емкостное и индуктивное сопротивления ведут
себя по-разному, но оба зависят от частоты. А что если соединить
последовательно катушку и конденсатор и подключить их к генератору частоты?
Как будет меняться реактивное сопротивление такой схемы при изменении частоты?
Конденсатор C и катушка L, соединенные последовательно, образуют так называемый
последовательный колебательный контур. В реальном контуре присутствует еще и
резистор R. Нет, специально резистор в контур конечно никто добавляет, но нужно
учитывать, например, сопротивление провода, которым намотана катушка.
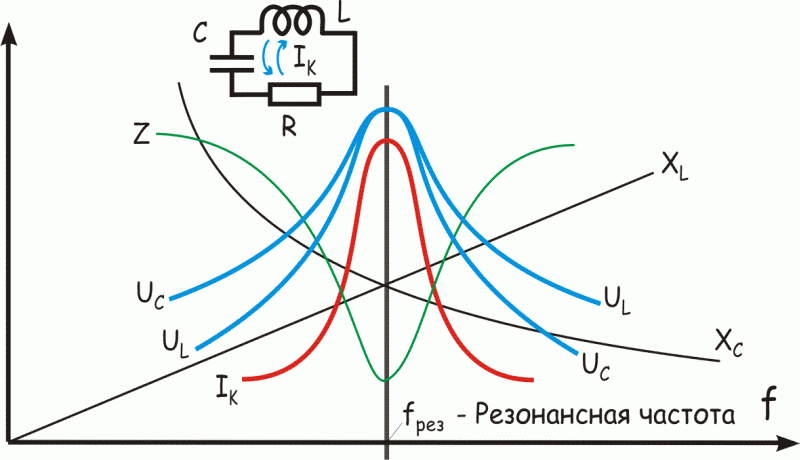
Для наглядности, изобразим все, что происходит в контуре, на графике, по горизонтальной оси будем откладывать частоту, по вертикально - значение токов, сопротивлений и напряжений. Мы уже знаем, что ёмкостное сопротивление (график XC) с увеличением частоты уменьшается, индуктивное, напротив, линейно растет (график XL). При некотором значении частоты fрез емкостное и индуктивное сопротивление будут одинаковы, и компенсируют друг друга, а общее реактивное сопротивление контура XLС=XL-XC будет равно нулю, а значит полное сопротивление контура будет минимальным и будет равно сопротивлению R (график Z). Частота fрез называется резонансной. На резонансной частоте резко возрастает ток в контуре и вместе с ним и напряжение на катушке UL и конденсаторе UC, также ставшими равными из-за равенства сопротивлений XL и XC.
Параллельный колебательный контур.
Теперь рассмотрим что происходит если соединить катушку L и конденсатор C
параллельно, также учитывая сопротивление R. Такое соединение называется
параллельный колебательный контур.
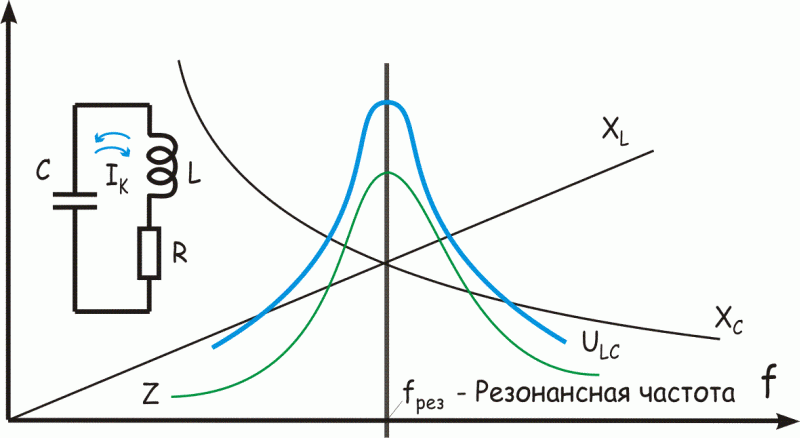
Общее сопротивление контура можно представить как параллельное соединение
двух сопротивлений XL и XC, а значит на резонансной
частоте fрез сопротивление контура будет максимально, а на частотах
больше или меньше резонансной - сопротивление контура будет уменьшаться и чем
дальше от резонансной частоты тем меньше будет сопротивление контура.
Следовательно напряжение, в полном соответвии с законом Ома, также будет
максимально на резонансной частоте (график ULC). Но самое интересное
что ток до контура будет минимальным, но внутри контура, так называемый
контурный ток будет достаточно велик.
Какие же процессы происходят внутри параллельного колебательного контура?
Для этого нам потребуется следующая схема:
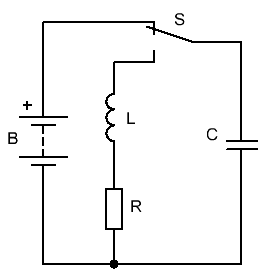
В исходном состоянии конденсатор C подключен к батарее B и через некоторое
время он полностью зарядится, между его обкладками накопится энергия, можно
сказать, что электроэнергия полученная конденсатором от батареи преобразуется в
энергию электрического поля. Теперь переключим конденсатор от батареи к
катушке L, создав тем самым параллельный колебательный LC-контур. Конденсатор
начнет разряжаться, напряжение на обкладках уменьшается, ток через катушку
нарастает и вокруг катушки образуется магнитное поле. Можно сказать, что
накопленная конденсатором энергия снова преобразуется в электрический ток,
который протекая через катушку преобразуется в магнитное поле катушки. Процесс
будет продолжаться пока конденсатор полностью на разрядится, а значит магнитное
поле вокруг катушки больше нечем будет удерживать и оно снова начнет
преобразовываться в электрический ток, вызывая появление ЭДС самоиндукции
обратной полярности, которая "помогает" удержаться уменьшающемуся току и
заряжает конденсатор, теперь уже в другой полярности. То есть вся накопленная
катушкой энергия преобразуется в электрическую, а та в свою очередь зарядит
конденсатор. Дальше процесс будет повторяться и он продолжался бы бесконечно,
если бы не внутреннее сопротивление контура R. Какая-то часть энергии,
преодолевая сопротивление R, будет преобразовываться в тепло и рассеиваться,
а значит электроэнергия в контуре будет постепенно уменьшаться, пока вся не
рассеется. Такой процесс называется затухающие колебания:
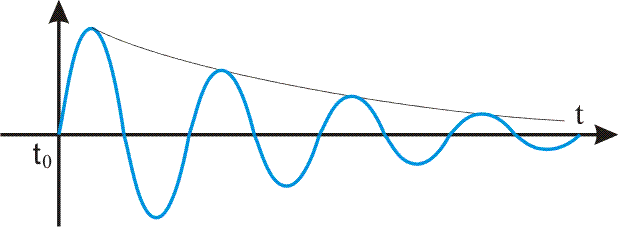
Любопытно то, что несмотря на то, что амплитуда колебаний уменьшается, частота
колебаний остается постоянной, и она равна резонансной частоте контура.
Частота этих колебаний в равной мере зависит от индуктивности катушки и
емкости конденсатора и вычисляется по формуле Томсона:
где Fрез - частота (Гц), L - индуктивность (Г), C - емкость (Ф).
Еще одна важная характеристика контура - добротность Q, которая говорит о том,
какая часть запасённой энергии теряется при каждом её перекачивании из
конденсатора в катушку и обратно. Чем больше потери, тем быстрее израсходуется
энергия, и тем быстрее затухнут колебания. Если потери будут очень большими -
колебания могут даже не начаться, конденсатор просто отдаст всю свою энегию,
которую сопротивление потерь превратит в тепло. Потери в контуре иногда
отображают двкмя условными сопротивлениями: RK1 - - включено
параллельно конденсатору и RK2 - включено последовательно с катушкой. и .
Чем больше RK1 и меньше RK2, тем меньше общие потери и
выше добротность Q. Часто все потери пересчитывают в одно сопротивление
RK, включая его последовательно с катушкой.
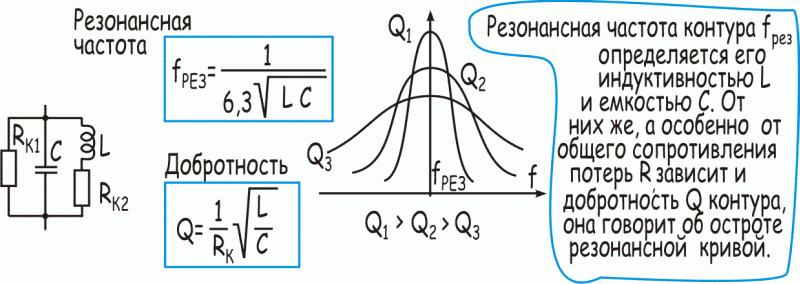
Кроме того, добротность Q зависит от соотношения L и C, для получения высокой
добротности желательно чтобы L было побольше, а C поменьше.
Copyright © R9AL 2020 Все права защищены
