Логический элемент

     Логический элемент - это такая схема, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе. Для каждого логического элемента можно составить таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов. Такая таблица называется таблица истинности.

Самый простой логический элемент - это элемент НЕ (NOT) - отрицание, или как его ещё называют - инвертор.

таблица истинности логического элемента НЕ:



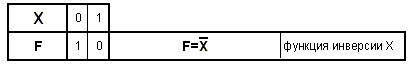
Логику работы элемента НЕ легко понять и запомнить, всего два логических состояния: если 0 на входе, то 1 на выходе, если 1 на входе, то 0 на выходе, логический элемент НЕ формирует на своем выходе противоположенный логический уровень.

А сколько вообще можно реализовать логический элементов с одним входом и с одним выходом?

Составим таблицу:



Функция F₁, её еще называют "генератор 0" формирует на выходе логического элемента логический ноль, не зависимо от того, что подается на вход. Тоже делает функция F₄, только она формирует единицу, не зависимо от того, что на входе. Функция F₃ нам уже знакома, это логическое НЕ, а вот функция F₂, повторитель, просто передает сигнал с входа на выход никак не меняя его. Обратите внимание, таблица истинности обладает обратной симметрией относительно горизонтальной оси, разделяющей таблицу по середине. Действительно, любую функцию нижней половины таблицы можно получить проинвертировав соответствующую функцию из верхней

F₄=!F₁, F₃=!F₂

     Фактически, любой из этих четырех элементов можно получить использую логический элемент НЕ. Для получения F₁ нужно просто вход элемента НЕ подключить к плюсовой шине питания, для получения элемента F₂ нужно взять два инвертора и подключить их друг за другом (двойное отрицание), F₃ - это сам элемент НЕ, и, наконец, чтобы получить F₄, нужно вход элемента НЕ соединить с минусовой шиной. Фактически, из всех четырех функция, нам нужен только инвертор, это единственная функция, с помощью которой можно получить оставшиеся три.

Рассмотрим теперь логический элемент у которого два входа и один выход:

Составим таблицу истинности для всех возможных логических элементов, имеющих два входа и один выход. Такая таблица будет содержать уже 16 возможных функций.



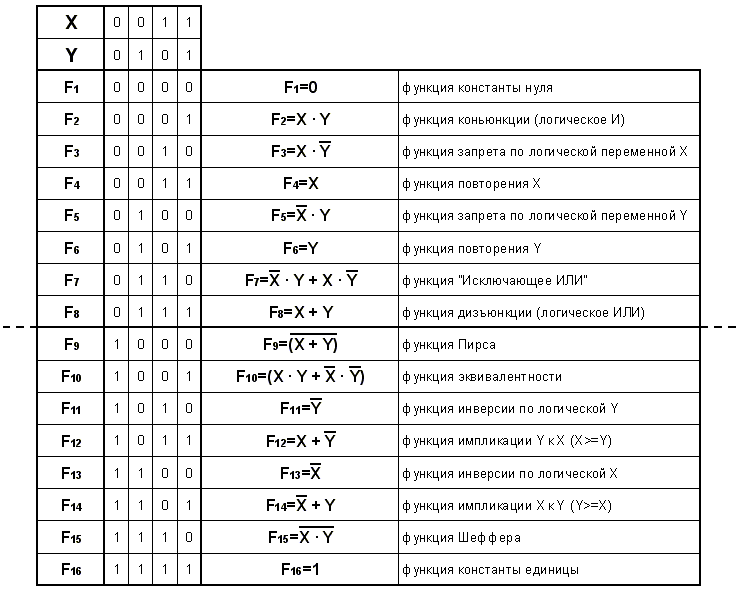
Логическая функция F₁ - это уже знакомый нам "генератор 0", независимо от того что на входе - на выходе всегда 0.

Логическая функция F₂ - это "логическое И" (AND), функция принимает значение 1 только тогда, когда на обоих входах тоже 1, в остальных случаях 0.



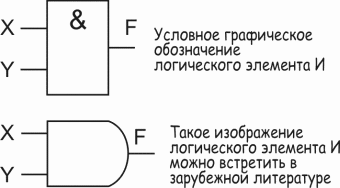
Логическая функция F₃ - это функция запрета по логической переменной X, если X=0 - на выходе 0, независимо от того что на входе Y, а если X=1, то на выходе всегда инвертированное значение Y.

Логическая функция F₄ - это функция повторения, выходное значение соответствует значению на входе X, независимо от того что на входе Y.

Логическая функция F₅ - аналогична функции F₃, только это функция запрета по логической переменной Y, если Y=0 - на выходе 0, независимо от того что на входе X, а если Y=1, то на выходе всегда инвертированное значение X.

Логическая функция F₆ - это функция повторения, выходное значение соответствует значению на входе Y, независимо от того что на входе X.

Логическая функция F₇ - это "Исключающее ИЛИ", функция принимает значение 0, когда на обоих одинаковые уровни, если уровни разные, то 1.



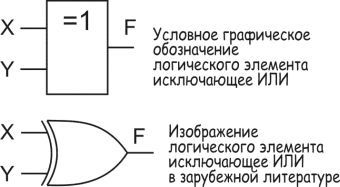
Логическая функция F₈ - это "логическое ИЛИ" (OR), функция принимает значение 0 только тогда, когда на обоих входах тоже 0, в остальных случаях 1.



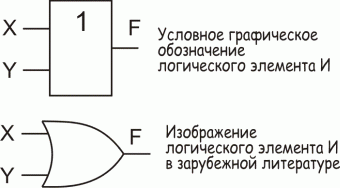
Логическая функция F₉ - это функция Пирса, или "инверсия логического ИЛИ", функция принимает значение 1 только тогда, когда на обоих входах тоже 0, в остальных случаях 0. Условное графическое обозначение аналогично изображению логического элемента И, но отличается наличием кружка на выходе, который обозначает инверсию.



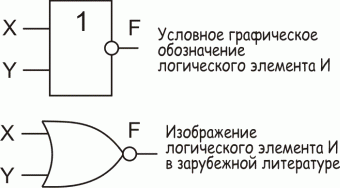
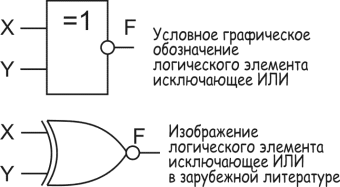
Логическая функция F₁₀ - функция эквивалентности, фактически это инверсия "Исключающего ИЛИ", поэтому графическое изображение это логического элемента аналогично логическому элементу "исключающее ИЛИ", только с символом инверсии на выходе. Функция принимает значение 1, когда на обоих входах одинаковые уровни, если уровни разные, то 0.



Логическая функция F₁₁ - это функция инверсии по Y, выходное значение соответствует инвертированному значению на входе Y, независимо от того что на входе X.

Логическая функция F₁₂ - это функция импликации Y к X, на выходе такого элемента 1 только тогда, когда X больше или равен Y.

Логическая функция F₁₃ - это функция инверсии по X, выходное значение соответствует инвертированному значению на входе X, независимо от того что на входе X.

Логическая функция F₁₄ - это функция импликации X к Y, на выходе такого элемента 1 только тогда, когда Y больше или равен X.

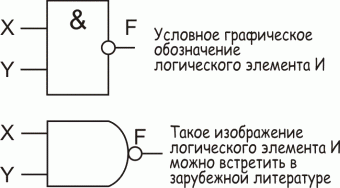
Логическая функция F₁₅ - это функция Шеффера, или "инверсия логического И", функция принимает значение 0 только тогда, когда на обоих входах 1, в остальных случаях на выходе 0. Условное графическое обозначение аналогично изображению логического элемента И, но отличается наличием символа инверсии на выходе.



Логическая функция F₁₆ - это уже знакомый нам "генератор 1", независимо от того что на входе - на выходе всегда 1.

Можно составить аналогичную таблицы для элементов с тремя, четырьмя и более входами, но сложность в том, что уже для трех-входового элемента таблица будет содержать 256 логических функций, для четырех-входового - 65536 ! Поэтому, мы ограничимся двухвходовыми элементами, так как любой более сложный элемент всегда можно представить как некоторую комбинацию двухвходовых.

Логический базис

     Логический базис - это функционально полный набор логических элементов, с помощью которого можно реализовать сколь угодно сложную логическую функцию.

Основных базисов известно четыре:

• Булев базис - содержит три элемента: И, ИЛИ, НЕ, с помощью которых можно создать любую функцию.
• Сокращенные булевы базисы - содержат два элемента:
  • Базис Шиффера (И, НЕ)
  • Базис Пирса (ИЛИ, НЕ)
• универсальные базисы - содержат один элемент:
  • Базис И-НЕ
  • Базис ИЛИ-НЕ
• Базис Жигалкина - содержит два элемента: И, Исключающее ИЛИ.

Действительно, любая логическая функция может быть записана с помощью всего трех логических операций: сложение (ИЛИ), умножение (И), инверсия (НЕ), в соответствии с формулой, например как представленные формулы в таблицах истинности. Это и есть булев базис.

Доказать истинность других базисов довольно просто, например в базисе Шиффера уже есть "И" и уже есть "НЕ", и можно реализовать элемент "ИЛИ", инвертировав оба входных сигналов (НЕ), перемножить их (И) и инвертировать еще раз (НЕ), в полном соответствии с теоремой де Моргана (см. урок 21. Точно также можно доказать справедливость базиса Пирса.

С универсальными базисами еще проще, мы можем из элементов "И-НЕ" и "ИЛИ-НЕ" создать элемент "НЕ", просто замкнув их входы.



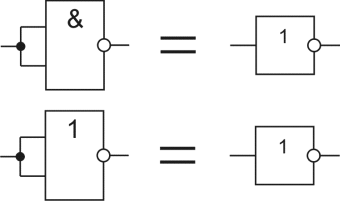
Сделать из элемента "И-НЕ" элемент "И" можно просто добавив к нему инвертор, который мы уже умеем делать, точно также можно из элемента "ИЛИ-НЕ" сделать элемент "ИЛИ":



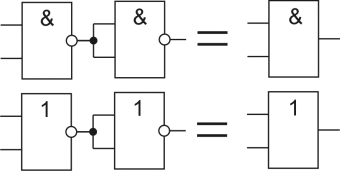
С помощью теоремы де Моргана, можем сделать и элемента "И-НЕ" элемент "ИЛИ", и наоборот, из элемента "ИЛИ-НЕ" элемент "И".



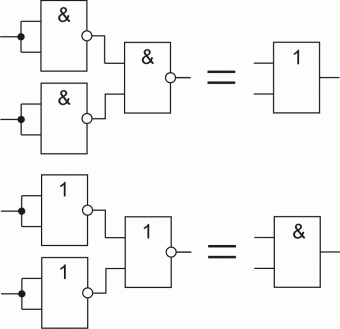
Аналогично можно привести к булеву базису и базис Жигалкина. Элемент "И" уже есть, а подав на один вход "Исключающего ИЛИ" логическую 1 - мы получим инвертор, сигнал поступающий на второй вход будет инвертироваться. Имея инввертор и элемент "И" - легко получить элемент "ИЛИ", по теореме де Моргана.







Copyright © R9AL 2020 Все права защищены

---